10 000 Divided By 100

In this and following sections we make use of the terms divisor, dividend, caliber, and residuum.

Divisor, Dividend, Quotient, and Residue

This schematic reminds readers of the position of these terms in the division procedure.

At present that these terms are divers, we begin the discussion of sectionalisation of decimal numbers. Suppose that nosotros wish to divide 637 by 100. We could do this in fraction form, change the result to a mixed fraction, so the mixed fraction to decimal form.

\[\frac{637}{100} = 6 \frac{37}{100} = 6.37\nonumber \]

We can also suit the division much as nosotros would the division of ii whole numbers.

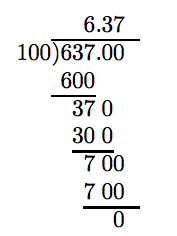
Note that adding two zeros after the decimal point in the dividend does non modify the value of 637. Farther, note that nosotros proceed equally if we are dividing 2 whole numbers, placing the decimal signal in the caliber directly to a higher place the decimal indicate in the dividend.

These observations lead to the following algorithm.

Dividing a Decimal past a Whole Number

To carve up a decimal number by a whole number, keep every bit follows:

1. Set the long sectionalization equally you would the partition of two whole numbers.
2. Perform the division every bit if the numbers were both whole numbers, adding zeros to the right of the decimal bespeak in the dividend as necessary to consummate the division.
3. Identify the decimal point in the quotient immediately above the decimal signal in the dividend.

Example 1

Divide 23 by 20.

Solution

Adapt as if using long segmentation to divide whole numbers, adding enough zeros to the right of the decimal signal in the dividend to complete the division.

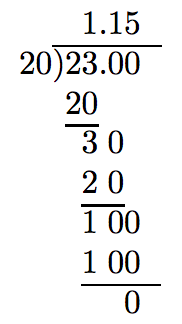
Hence, 23 divided by 20 is 1.15.

Calculation Zeroes to the Correct of the Decimal Point

Normally, one does non immediately see how many zeros to the correct of the decimal point in the dividend are needed. These zeros are usually added at each pace of the partition, until the partition is completed or the user is willing to terminate the process and accept just an estimate of the quotient.

Example 2

Divide: 155.ii ÷ 25.

Solution

Arrange as if using long division to dissever whole numbers, and begin.

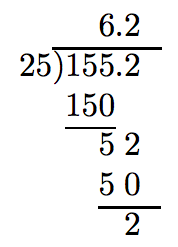
We however have a nonzero remainder. Calculation another zero does no proficient.

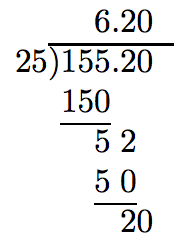
However, if we add together one more boosted nix, the division completes with a zero residuum.

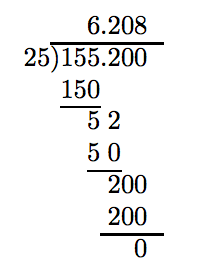
Thus, 155.two divided past 25 is half-dozen.208.

Practice

Divide: 42.55 ÷ 23

Answer

1.85

Decimal Divisors When the divisor contains a decimal bespeak, we take a little piece of work to do before we begin the segmentation process. Suppose that we wish to divide 1.25 by 2.five. In fraction form, nosotros could starting time with

\[ \frac{one.25}{ii.v},\nonumber \]

then clear the decimals from the denominator past multiplying both numerator and denominator by 10. Note: Recall that multiplying by x moves the decimal point one place to the right.

\[ \begin{aligned} \frac{one.25}{2.five} = \frac{1.25 \cdot 10}{ii.5 \cdot 10} \\ = \frac{12.5}{25} \end{aligned}\nonumber \]

Thus, dividing 1.25 by 2.5 is equivalent to dividing 12.v past 25. This we know how to do.

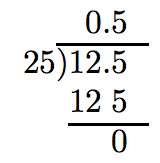
Thus, 1.25 divided past 2.v is 0.5.

Writing Mathematics

Never write .5. Always add the leading zero in the ones identify and write 0.five.

Instead of working in fraction class, we can accept care of positioning the decimal point in the long segmentation framework. Start with:

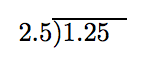
Move the decimal point in the divisor to the finish of the divisor, then motion the decimal betoken in the dividend an equal number of places.

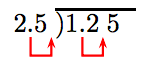
Thus, the division becomes

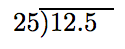
and we proceed as to a higher place to find the quotient. This discussion motivates the following algorithm.

Dividing by a Decimal Divisor

If the divisor contains a decimal, proceed every bit follows:

1. Move the decimal to the end of the divisor.
2. Move the decimal in the dividend an equal number of places.

We can then consummate the division using the rules for dividing a decimal by a whole number.

Instance three

Divide: \(\overline{ )4.392}\)

Solution

Motion the decimal in the divisor to the end of the divisor. Movement the decimal in the dividend an equal number of places (ii places) to the right.

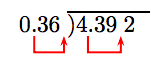
At present nosotros can follow the algorithm for dividing a decimal number past a whole number.

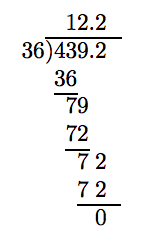
Thus, 4.392 divided by 0.36 is 12.2.

Practise

Divide: \(0.45 \overline{)36.99}\)

Respond

82.2

Dividing Signed Decimal Numbers

The rules governing division of signed decimal numbers are identical to the rules governing sectionalization of integers.

Like Signs. The quotient of two decimal numbers with similar signs is positive. That is:

\[\frac{(+)}{(+)} = + \text{ and } \frac{(−)}{(−)} = +\nonumber \]

Unlike Signs. The quotient of two decimal numbers with unlike signs is negative. That is:

\[\frac{(+)}{(−)} = − \text{ and } \frac{(−)}{(+)} = −\nonumber \]

Example 4

Divide: −0.03 ÷ 0.024.

Solution

Commencement, divide the magnitudes. Motion the decimal in the divisor to the end of the divisor. Motility the decimal in the dividend an equal number of places (three places) to the correct. Note that this requires an extra trailing nix in the dividend.

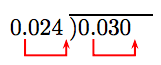
Our problem and so becomes:

\[ 24 \overline{24 )xxx}\)

Nosotros can at present follow the algorithm for dividing a decimal number by a whole number. Notation that nosotros have to add two trailing zeros in the dividend to complete the division with a goose egg remainder.

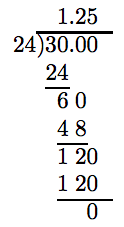
Finally, because the quotient of different signs is negative, −0.03 divided by 0.024 is −1.25. That is,

\[ \frac{-0.03}{0.024} = -1.25.\nonumber \]

Exercise

Divide: −0.0113 ÷ 0.05

Answer

−0.226

Rounding

Sometimes an verbal decimal representation of a fraction is not needed and is an approximation is more than adequate.

Example 5

Convert 4/7 to a decimal. Round your answer to the nearest hundredth.

Solution

Nosotros need to conduct the segmentation one place beyond the hundredths place.

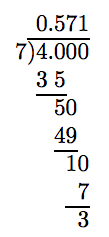
To round to the nearest hundredth, first identify the rounding and exam digits.

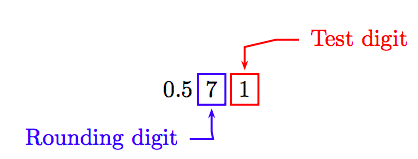
Considering the "test digit" is less five, leave the rounding digit alone and truncate. Therefore, correct to the nearest hundredth, 4/vii ≈ 0.57.

Practice

Convert v/7 to a decimal. Round your answer to the nearest hundredth.

Answer

0.71

Dividing by Powers of 10

Recall:

\[\brainstorm{aligned} 10^1 = x \\ ten^two = 10 \cdot ten = 100 \\ 10^iii = 10 \cdot 10 \cdot ten = 1000 \end{aligned}\nonumber \]

Powers of X

In the expression 10n, the exponent matches the number of zeros in the respond. Hence, 10n will be a ane followed by due north zeros.

Thus, 10⁴ = 10, 000, 10^v = 100, 000, etc. The exponent tells united states how many zeros volition follow the 1.

Let's dissever 123456.seven by yard.

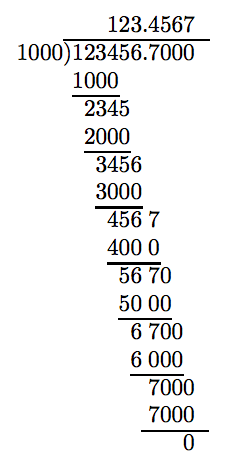
Note the consequence: 123456.7 divided by one thousand is 123.4567. Dividing by k moves the decimal signal 3 places to the left!

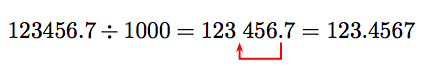
This discussion leads to the following effect.

Dividing a Decimal by a Ability of Ten

Dividing a decimal number past 10n volition move the decimal signal n places to the left.

Example 6

Simplify: 123456.7 ÷ 10^four

Solution

Dividing past 10⁴ (or equivalently, 10,000) moves the decimal point four places to the left. Thus, 123456.seven ÷ 10^four = 12.34567.

Exercise

Simplify: 123456.7 ÷ 10²

Answer

1234.567

Guild of Operations

We remind readers of the Rules Guiding Society of Operations.

Rules Guiding Society of Operations

When evaluating expressions, keep in the following order.

1. Evaluate expressions independent in group symbols first. If grouping symbols are nested, evaluate the expression in the innermost pair of group symbols first.
2. Evaluate all exponents that appear in the expression.
3. Perform all multiplications and divisions in the order that they appear in the expression, moving left to right.
4. Perform all additions and subtractions in the order that they appear in the expression, moving left to correct.

In addition, when fractions are present:

Fractional Expressions

If a partial expression is nowadays, simplify the numerator and denominator separately, and so divide.

Case vii

Evaluate ab/(c + d), given that a = 2.1, b = −iii.four, c = −1.three, and d = 1.1.

Solution

Recall that it is good do to prepare an expression for commutation by using parentheses.

\[ab/(c + d) = (~)(~)/((~) +(~)) \nonumber \]

Substitute the given values for a, b, c, and d, then use the Rules Guiding Gild of Operations to simplify the resulting expression.

\[ \begin{aligned} ab/(c+d) = (2.one)(-3.4)/((-one.3)+(1.1)) ~ & \textcolor{reddish}{ii.1, -3.four,-one.iii, ane.ane \text{ for } a, b, c, d.} \\ = (2.one)(-3.4)/(-0.2) ~ & \textcolor{scarlet}{ \text{ Parens: } (-one.3) + (1.ane) = -0.ii.} \\ =-seven.fourteen/(-0.2) ~ & \textcolor{cerise}{ \text{ Multiply: } (2.1)(-3.iv) = -7.14.} \\ =35.7 ~ & \textcolor{red}{ \text{ Separate: } -seven.14/(-0.2) = 35.7} \end{aligned}\nonumber \]

Practice

If a = −2.ane, b = one.7, c = 4, and d = 0.05, evaluate:

\[\frac{a+b}{cd}\nonumber \]

Answer

−two

Example 8

Given a = 0.ane and b = −0.3, evaluate the expression

\[\frac{a+2b}{2a+b}.\nonumber \]

Solution

Substitute the given values, then use the Rules Guiding Social club of Operations to simplify the resulting expression.

\[ \begin{aligned} \frac{a+2b}{2a+b} = \frac{(0.one)+2(-0.3)}{2(0.1)+(-0.3)} ~ & \textcolor{red}{ \text{ 0.1 for } a,~ -0.3 \text{ for } b.} \terminate{aligned}\nonumber \]

Simplify the numerator, simplify the denominator, then carve up.

\[ \begin{aligned} = \frac{0.ane+(-0.6)}{0.2+(-0.3)} ~ & \textcolor{carmine}{ \begin{aligned} \text{ Numerator: } 2(-0.3) = -0.6. \\ \text{ Denominator: } 2(0.1)=0.two. \cease{aligned}} \\ = \frac{-0.v}{-0.1} ~ & \textcolor{ruby-red}{ \begin{aligned} \text{ Numerator: } 0.1 + (-0.6)=-0.5 \\ \text{ Denominator: } 0.2 + (-0.3) = -0.1. \finish{aligned}} \\ =5 ~ & \textcolor{blood-red}{ \text{ Divide: } -0.five/(-0.1)=5.} \end{aligned}\nonumber \]

Do

If a = 0.v and b = −0.125, evaluate:

\[ \frac{2a-b}{a+2b}\nonumber \]

Answer

4.5

Exercises

In Exercises 1-xvi, divide the numbers.

i. \(\frac{39}{52}\)

2. \(\frac{xvi}{25}\)

iii. \(\frac{755.three}{83}\)

four. \(\frac{410.4}{76}\)

five. \(\frac{333}{74}\)

6. \(\frac{117}{65}\)

7. \(\frac{32.12}{73}\)

eight. \(\frac{12.32}{44}\)

nine. \(\frac{37.63}{71}\)

x. \(\frac{xx.46}{31}\)

xi. \(\frac{138}{92}\)

12. \(\frac{110}{25}\)

13. \(\frac{17}{25}\)

14. \(\frac{18}{75}\)

fifteen. \(\frac{229.5}{51}\)

xvi. \(\frac{525.6}{72}\)

---

In Exercises 17-40, divide the decimals.

17. \(\frac{0.3478}{0.47}\)

18. \(\frac{0.4559}{0.97}\)

19. \(\frac{one.694}{ii.two}\)

twenty. \(\frac{1.008}{ane.8}\)

21. \(\frac{43.61}{four.9}\)

22. \(\frac{22.78}{3.4}\)

23. \(\frac{1.107}{0.41}\)

24. \(\frac{2.465}{0.29}\)

25. \(\frac{2.958}{0.51}\)

26. \(\frac{5.141}{0.53}\)

27. \(\frac{71.76}{seven.eight}\)

28. \(\frac{14.08}{8.eight}\)

29. \(\frac{0.8649}{0.93}\)

30. \(\frac{0.3901}{0.83}\)

31. \(\frac{0.6958}{0.71}\)

32. \(\frac{0.1829}{0.31}\)

33. \(\frac{one.248}{0.52}\)

34. \(\frac{6.375}{0.85}\)

35. \(\frac{62.56}{9.ii}\)

36. \(\frac{28.08}{vii.8}\)

37. \(\frac{6.278}{eight.6}\)

38. \(\frac{3.185}{four.9}\)

39. \(\frac{two.698}{7.1}\)

40. \(\frac{4.959}{8.7}\)

---

In Exercises 41-64, divide the decimals.

41. \(\frac{−11.04}{1.6}\)

42. \(\frac{−31.27}{5.3}\)

43. \(\frac{−3.024}{v.half-dozen}\)

44. \(\frac{−iii.498}{5.three}\)

45. \(\frac{−0.1056}{0.22}\)

46. \(\frac{−0.2952}{−0.72}\)

47. \(\frac{0.3204}{−0.89}\)

48. \(\frac{0.3306}{−0.38}\)

49. \(\frac{−ane.419}{0.43}\)

50. \(\frac{−ane.625}{−0.25}\)

51. \(\frac{−sixteen.72}{−2.2}\)

52. \(\frac{−66.24}{ix.2}\)

53. \(\frac{−2.088}{−0.87}\)

54. \(\frac{−ii.025}{−0.75}\)

55. \(\frac{−ane.634}{−viii.6}\)

56. \(\frac{−three.094}{3.4}\)

57. \(\frac{−0.119}{0.85}\)

58. \(\frac{0.5766}{−0.62}\)

59. \(\frac{−iii.591}{−half dozen.3}\)

threescore. \(\frac{−3.016}{five.eight}\)

61. \(\frac{36.96}{−4.iv}\)

62. \(\frac{−78.26}{−8.half dozen}\)

63. \(\frac{−2.156}{−0.98}\)

64. \(\frac{−6.072}{0.66}\)

---

In Exercises 65-76, divide the decimal by the given power of 10.

65. \(\frac{524.35}{100}\)

66. \(\frac{849.39}{100}\)

67. \(\frac{563.94}{ten^3}\)

68. \(\frac{884.fifteen}{10^three}\)

69. \(\frac{116.81}{10^two}\)

70. \(\frac{578.01}{x^3}\)

71. \(\frac{694.55}{x}\)

72. \(\frac{578.68}{100}\)

73. \(\frac{341.16}{10^3}\)

74. \(\frac{46.63}{10^four}\)

75. \(\frac{113.02}{1000}\)

76. \(\frac{520.77}{k}\)

---

77. Compute the quotient 52/83, and round your reply to the nearest tenth.

78. Compute the quotient 43/82, and round your reply to the nearest tenth.

79. Compute the quotient 51/59, and round your answer to the nearest tenth.

lxxx. Compute the quotient 17/69, and circular your answer to the nearest tenth.

81. Compute the quotient 5/74, and round your answer to the nearest hundredth.

82. Compute the caliber iii/41, and round your reply to the nearest hundredth.

83. Compute the quotient 5/94, and circular your answer to the nearest hundredth.

84. Compute the caliber 3/75, and round your respond to the nearest hundredth.

85. Compute the caliber 7/72, and circular your answer to the nearest hundredth.

86. Compute the quotient 4/57, and round your answer to the nearest hundredth.

87. Compute the caliber 16/86, and round your answer to the nearest 10th.

88. Compute the quotient 21/38, and round your answer to the nearest tenth.

---

In Exercises 89-100, simplify the given expression.

89. \(\frac{vii.5 \cdot 7.1 − 19.5}{0.54}\)

90. \(\frac{ane.5(−8.8) − (−18.six)}{1.8}\)

91. \(\frac{17.76 − (−11.7)}{0.52}\)

92. \(\frac{−14.8 − 2.ane}{2.62}\)

93. \(\frac{−18.22 − 6.7}{14.75 − vii.75}\)

94. \(\frac{ane.four − 13.25}{−vi.84 − (−2.i)}\)

95. \(\frac{−12.9 − (−10.98)}{0.v^two}\)

96. \(\frac{5.1 − (−16.five)}{(−1.5)^ii}\)

97. \(\frac{−ix.5 \cdot 1.6 − three.seven}{−3.vi}\)

98. \(\frac{6.v(−1.6) − 3.35}{−ii.75}\)

99. \(\frac{−14.98 − 9.6}{17.99 − 19.99}\)

100. \(\frac{−5.half dozen − vii.5}{−5.05 − 1.5}\)

---

101. Given a = −ii.21, c = 3.3, and d = 0.5, evaluate and simplify the following expression.

\[\frac{a − c}{d^2}\nonumber \]

102. Given a = two.viii, c = −14.68, and d = 0.5, evaluate and simplify the following expression.

\[\frac{a − c}{d^ii}\nonumber \]

103. Given a = −5.8, b = ten.37, c = 4.eight, and d = 5.64, evaluate and simplify the post-obit expression:

\[\frac{a − b}{c − d}\nonumber \]

104. Given a = −x.79, b = 3.94, c = −3.two, and d = −8.11, evaluate and simplify the following expression:

\[\frac{a − b}{c − d}\nonumber \]

105. Given a = −1.5, b = iv.7, c = eighteen.8, and d = −11.75, evaluate and simplify the following expression.

\[\frac{ab − c}{d}\nonumber \]

106. Given a = nine.3, b = 6.6, c = xiv.27, and d = 0.2, evaluate and simplify the following expression.

\[\frac{ab − c}{d}\nonumber \]

---

107. Biodiesel plants. There are about 180 biodiesel plants operating in about 40 states. Of the states that have them, what is the average number of biodiesel plants per state? Associated Press-Times-Standard 01/02/10 Fledgling biofuel industry ends year on a bleak note.

108. Bat fungus. A fungus called "white-nose syndrome" has killed an estimated 500,000 bats throughout the country. This means nigh 2,400,000 pounds of bugs aren't eaten over the year, says Forest Service biologist Becky Ewing. How many pounds of insects does an average bat swallow annually? Associated Press-Times-Standard 5/ii/09

109. Patent backlog. In the U.S. Patent and Trademark Office, 6000 examiners have a excess of 770,000 new, unexamined applications for patents. How many applications is that for each examiner to grab up on? Round your reply to the nearest tenth. Associated Press-Times-Standard v/v/09

110. Doing well. The big wellness insurer Wellpoint, Inc., owner of Anthem Blue Cross, earned $536 million in the concluding three months of 2009. What was the average earnings per month for the insurer over that period? Circular to the nearest million. Associated Press-Times-Standard 02/09/x HHS secretary asks Anthem Blue Cross to justify rate hike.

111. Cyber attacks. The Pentagon has spent $100 meg over a half dozen-month period responding to and repairing damage from cyber-attacks and other reckoner network issues. What's the boilerplate amount of money spent per month over that fourth dimension? Round your answer to the nearest hundredth of a million. Associated Press-Times-Standard 4/19/09

112. Daily milk. The boilerplate California cow tin produce 2,305 gallons of milk annually. How much milk can a cow produce each day? Circular your answer to the nearest hundredth of a gallon. www.moomilk.com/faq.htm

113. Media mail. To promote her business organization, Theresa mails several packages via Media Postal service. Ane package weighing 2 lbs. costs $2.77, another package weighing three lbs. costs $3.16, and the third package weighing 5 lbs. costs $3.94 to mail. What was the boilerplate cost per pound to mail the packages? Round your result to the nearest penny. www.usps.com/prices/media-mailprices.htm

---

Answers

one. 0.75

3. ix.one

5. 4.5

7. 0.44

9. 0.53

11. i.five

13. 0.68

15. 4.5

17. 0.74

xix. 0.77

21. 8.nine

23. 2.7

25. 5.8

27. 9.2

29. 0.93

31. 0.98

33. 2.4

35. half dozen.viii

37. 0.73

39. 0.38

41. −6.nine

43. −0.54

45. −0.48

47. −0.36

49. −3.3

51. 7.6

53. 2.4

55. 0.nineteen

57. −0.14

59. 0.57

61. −8.4

63. 2.2

65. five.2435

67. 0.56394

69. one.1681

71. 69.455

73. 0.34116

75. 0.11302

77. 0.6

79. 0.nine

81. 0.07

83. 0.05

85. 0.10

87. 0.2

89. 62.5

91. 117.84

93. −3.56

95. −vii.68

97. 5.25

99. 12.29

101. −22.04

103. 19.25

105. ii.2

107. 4.v biodiesel plants

109. 128.3

111. $16.67 million

113. $0.99 per pound

10 000 Divided By 100,

Source: https://math.libretexts.org/Bookshelves/PreAlgebra/Book:_Prealgebra_%28Arnold%29/05:_Decimals/5.05:_Dividing_Decimals

Posted by: cooperallontention63.blogspot.com

Share this post